وبلاگ دانشجویان ارشد کامپیوتر لرستان
تبادل جزوات درسی و خبرنامه دانشجویان ارشد کامپیوتر لرستانوبلاگ دانشجویان ارشد کامپیوتر لرستان
تبادل جزوات درسی و خبرنامه دانشجویان ارشد کامپیوتر لرستانوبلاگ های ارشد کامپیوتر
- وبلاگ دانشجویان ارشد کامپیوتر خرم آباد تبادل نظرات و جزوه های درسی دانشجویان ارشد کامپیوتر خرم آباد
- ارشدکامپیوتر علوم تحقیقات (ورودی بهمن91)
- وبلاگ دانشجویان کارشناسی ارشد نرم افزار
- گروه کارشناسی ارشد نرم افزار واحد خرم آباد وبلاگ مهندس صالحی
- وبلاگ دانشجویان کارشناسی ارشد نرم افزار وبلاگ دانشجویان کارشناسی ارشد ورودی 92 نرم افزار دانشگاه علوم تحقیقات لرستان
- وبلاگ دانشجویان کامپیوتر - ورودی 91 وبلاگ دانشجویان کامپیوتر علوم تحقیقات لرستان
- واحد علوم تحقیقات خرم آباد
- دانشجویان کارشناسی ارشد کامپیوتر نرم افزار دانشگاه آزاد اسلامی خرم آباد وبلاگ مهندس رحمانی
دستهها
ابر برجسب
ریاضیاتجدیدترین یادداشتها
همهنویسندگان
- م سهرابی نیا 52
بایگانی
تقویم
آبان 1394| ش | ی | د | س | چ | پ | ج |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
جستجو
الگوریتم استراسن
الگوریتم استراسن
والکر استراسن الگوریتم استراسن را در سال ۱۹۶۹ منتشر کرد. اگرچه الگوریتم او فقط کمی سریع تر از الگوریتمهای استاندارد برای ضرب ماتریس است، اما او اولین کسی بود که اشاره کرد رویکرد استاندارد مطلوب نمیباشد. مقالهٔ او به جستجوی الگوریتمهای سریعتر مانند الگوریتم پیچیده تر Coppersmith–Winograd منتشر شده در سال ۱۹۸۷ پرداخت.
الگوریتم
ستون سمت چپ، ضرب ماتریسی ۲x۲ را نشان میدهد. ضرب ماتریسی Naïve به یک
ضرب برای هر “۱” از ستون سمت چپ نیاز دارد. هر یک از ستونهای دیگر نشان
دهندهٔ یک واحد از ۷ ضرب در الگوریتم میباشند و از مجموع ستونها، ضرب
ماتریس کامل در سمت چپ حاصل میشود.
بگذارید A،B دو ماتریس مربعی در یک حلقه R باشند. ما میخواهیم حاصل ماتریس C را به صورت زیر محاسبه کنیم:
اگر ماتریسهای A،B از نوع ۲n x ۲n نباشند، ما ردیفها و ستونهای خالی را با صفر پر میکنیم.
ما A،B و C را به ماتریسهای بلوکی هم سایز تجزیه میکنیم.
ما با این ساختار، تعداد ضربها را کاهش ندادیم. هنوز هم به ۸ ضرب نیاز داریم تا ماتریسهای Ci،j را محاسبه کنیم، زمانی که از ضرب ماتریسی استاندارد استفاده میکنیم نیز به همان تعداد ضرب نیاز داریم.
حالا بخش مهم در اینجا آمدهاست. ما ماتریسهای جدید را به شرح زیر تعریف میکنیم:
که سپس برای بیان Ci،j به صورت Mk مورد استفاده قرار میگیرند. با تعریف مان از Mk میتوانیم یک ضرب ماتریس را حذف کنیم و تعداد ضربها را به ۷ کاهش دهیم (یک ضرب برای هر Mk) و Ci،j را به صورت زیر بیان کنیم:
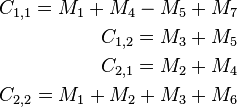
ما این فرایند تقسیم را n بار تکرار میکنیم تا زمانی که ماتریسهای فرعی به اندازه کافی کوچک شده و قابل تقسیم نباشند. (اجزای حلقه R).
کاربردهای عملی الگوریتم استراسن با روشهای استاندارد ضرب ماتریسی برای ماتریسهای فرعی کوچک تعویض شدند که آن الگویتمها برایشان موثرتر میباشند. نقطه هم گذری خاص که الگوریتمهای استراسن برایشان موثرتر است به کاربرد و سختافزار ویژه بستگی دارد.
پیچیدگی مجانبی
ضرب ماتریسی استاندارد تقریباً عملیات محاسباتی ۲n^۳ (که n=۲^n) (جمعها و ضربها) را میپذیرد؛ پیچیدگی مجانبی (O(N۳میباشد. تعداد جمعها و ضربهای مورد نیاز در الگوریتم استراسن را میتوان به صورت زیر محاسبه کرد:
اجازه دهید (f(n تعداد عملیات برای یک ماتریس ۲n × ۲n باشد. آنگاه با عملیات بازگشتی الگوریتم استراسن میبینیم که برای برخی l ثابت که به تعداد جمعهای انجام شده در هر عملیات الگوریتم وابستهاست. یعنی پیچیدگی مجانبی برای ضرب ماتریسها با استفاده از الگوریتم استراسن به شرح زیر است:
هرچند کاهش در تعداد عملیات محاسباتی تا حدودی به بهای کاهش ثبات عددی میباشد.
منابع
- استراسن، ولکر، حذف گاوسی مطلوب نیست، ص ۳۵۴-۳۵۶، ۱۹۶۹
- تامس اچ. کردمن، چارلز ای. لایسرسون، رانلد ال. روست، کلیفورد استاین، آشنایی با الگوریتم، ویرایش دوم، انتشارات ام آی تی، فصل ۲۸، الگوریتم استراسن برای ضرب ماتریس، ص ۷۳۴-۷۴۱، ۲۰۰۱